爱问经验方法/步骤
1/7分步阅读把方程看成y的二次方程，由判别式为非负数求解出函数的定义域。
[图]2/7使用导数来解析函数的单调性，计算曲线方程的一阶导数，即可求出函数的驻点。
[图]3/7根据驻点的符号，判断一阶导数的正负，即可计算出函数的单调增区间和减区间。
[图]4/7用导数解析函数的凸凹性，计算函数的二阶导数，进一步有函数的拐点，即可判断函数的凸凹性。
[图]5/7如果一个函数f(x)在某个区间I上有f''(x)(即二阶导数)>0恒成立，那么在区间I上f(x)的图像上的任意两点连出的一条线段，这两点之间的函数图像都在该线段的下方，反之在该线段的上方。
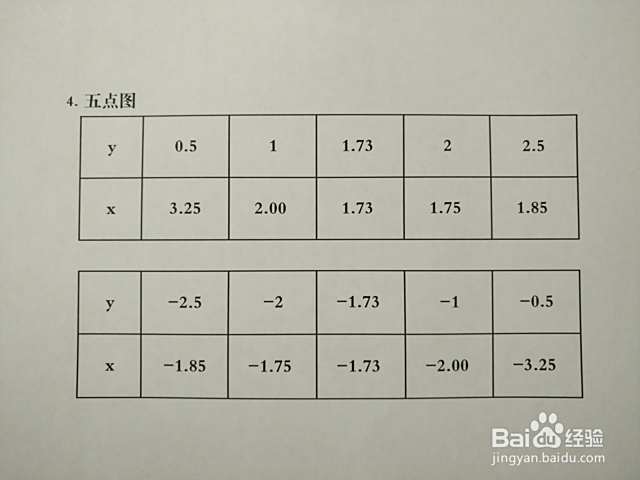
6/7列举以x值来表示y值，可知有两个不同的x值对应y值，曲线上部分点图表如下。
[图]7/7根据以上函数的定义域、单调性、凸凹性等性质，并结合函数的单调区间和凸凹区间，函数的示意图如下：
[图]编辑于2025-09-23，内容仅供参考并受版权保护
